2. Desenvolupament
Aprenem nous sabers
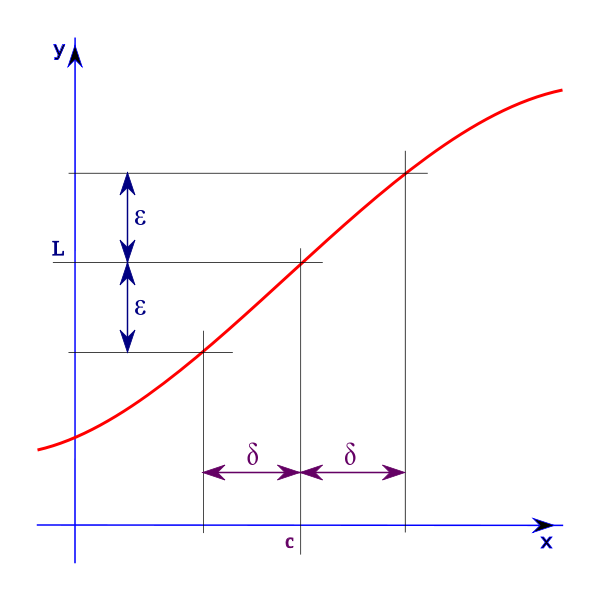 Ara que ja heu identificat les funcions que modelitzen les dades de producció de l'empresa, és hora de profunditzar en l'estudi d'aquestes funcions. Aprendreu a calcular límits, asímptotes i derivades, eines fonamentals per a l'optimització i la resolució de problemes.
Ara que ja heu identificat les funcions que modelitzen les dades de producció de l'empresa, és hora de profunditzar en l'estudi d'aquestes funcions. Aprendreu a calcular límits, asímptotes i derivades, eines fonamentals per a l'optimització i la resolució de problemes.
Instruccions:
- Agrupament: Individual
- Temporització: 2 hores
Tasques a realitzar:
-
Estudi de límits: Comença estudiant els conceptes de límit de funcions racionals. Utilitza les funcions que has identificat en l'activitat anterior i calcula els seus límits en els punts crítics que identifiquis. Recorda que els límits són fonamentals per determinar el comportament de les funcions en diferents punts.
- Producte: Conjunt de càlculs de límits amb les seves respectives funcions.
-
Càlcul d'asímptotes: A continuació, usa aquest coneixement per calcular les asímptotes horitzontals i verticals de les funcions que has identificat. Aquestes asímptotes t'ajudaran a comprendre el comportament de la funció a mesura que s'acosta a certs valors.
- Producte: Conjunt de càlculs d'asímptotes amb les seves respectives funcions.
-
Càlcul de derivades: Finalment, calcula les derivades de les funcions que has identificat. Les derivades són crucials per determinar on una funció és creixent o decreixent, informació que és fonamental per a l'optimització.
- Producte: Conjunt de càlculs de derivades amb les seves respectives funcions.
-
Estudi de les propietats de les funcions mitjançant les derivades: Després d'haver calculat les derivades, utilitza-les per estudiar la continuïtat, la derivabilitat, els extrems relatius, i el creixement i decreixement de les teves funcions.
- Producte: Conjunt d'anàlisi sobre les propietats de les funcions estudiades.
Al final d'aquesta activitat, hauries d'haver adquirit una comprensió més profunda de les funcions que estàs estudiant, que et prepararà per a l'activitat final d'optimització.
Rúbrica
| Nivell d'acompliment: Baix | Nivell d'acompliment: Mitjà | Nivell d'acompliment: Alt | |
|---|---|---|---|
| Càlcul de límits | Els càlculs de límits contenen errors significatius o falten completament (1) | Els càlculs de límits són majoritàriament correctes, però poden contenir errors menors (2) | Els càlculs de límits són precisos i complets (3) |
| Càlcul d'asímptotes | Els càlculs d'asímptotes contenen errors significatius o falten completament (1) | Els càlculs d'asímptotes són majoritàriament correctes, però poden contenir errors menors (2) | Els càlculs d'asímptotes són precisos i complets (3) |
| Càlcul de derivades | Els càlculs de derivades contenen errors significatius o falten completament (1) | Els càlculs de derivades són majoritàriament correctes, però poden contenir errors menors (2) | Els càlculs de derivades són precisos i complets (3) |
| Estudi de propietats de funcions | Els estudi de propietats conté errors significatius o falten completament (1) | Els estudi de propietats són majoritàriament correctes, però poden contenir errors menors (2) | Els estudi de propietats són precisos i complets (3) |
| Aplicació de coneixements | L'aplicació dels coneixements a problemes pràctics és limitada o inexacta (1) | L'aplicació dels coneixements a problemes pràctics és competent, però pot no ser totalment precisa o completa (2) | L'aplicació dels coneixements a problemes pràctics és completa, precisa i demostra una comprensió profunda del material (3) |
- Activitat
- Nom
- Data
- Puntuació
- Notes
- Reinicia
- Imprimeix
- Aplica
- Finestra nova
Llicenciat sota la Llicència Creative Commons Reconeixement NoComercial CompartirIgual 4.0
](https://mermaid.live/edit#pako:eNqVkt1qwjAUgF8lnJttUMVYm2ouBv5U2cVgsF2N3oQmaqBtSprInPVd9gJ7Cl9sWR21Chsz5CI5-c5HTnJ2kCgugMJKs2KNXiZxjtwY38YwXmlbsEzkhqKHnMuN5JalMdyhTue-6qO10qKs0MShUWksl4gLlB4-M2lKRx1Fkxp-0orbxAiKpoePNLFp2WIrNHWKnwPEb1jp4oVRRpw00181bbxCs7ZJuKnlhvGWaPbHfRq6QtFZUYVWhRSGteqKLjzj3IlkeYFXaO5Ec3ndcyzOc_5b--KqCh0NHmRCZ0xy9_-77-wYzFpkIgbqllwsmU1NDHG-dyizRj1v8wSo0VZ4YAvOjJhJ5jonA7pkadlEIy6N0k2wYPmrUidI1MePx8ar-69mgO7gDSjGQZf44dDvkwEmPRwQD7YuHPrdwO17ZEBGYZ8EZO_Be63tdcNRQEZ4gP3hkGAfB_svcFLzNA)